Monoton. Streng Monoton? - Mathe ist doch immer monoton!
Was monoton bedeutet, was streng monoton wirklich meint – und warum der Unterschied nicht nur in der Theorie zählt.
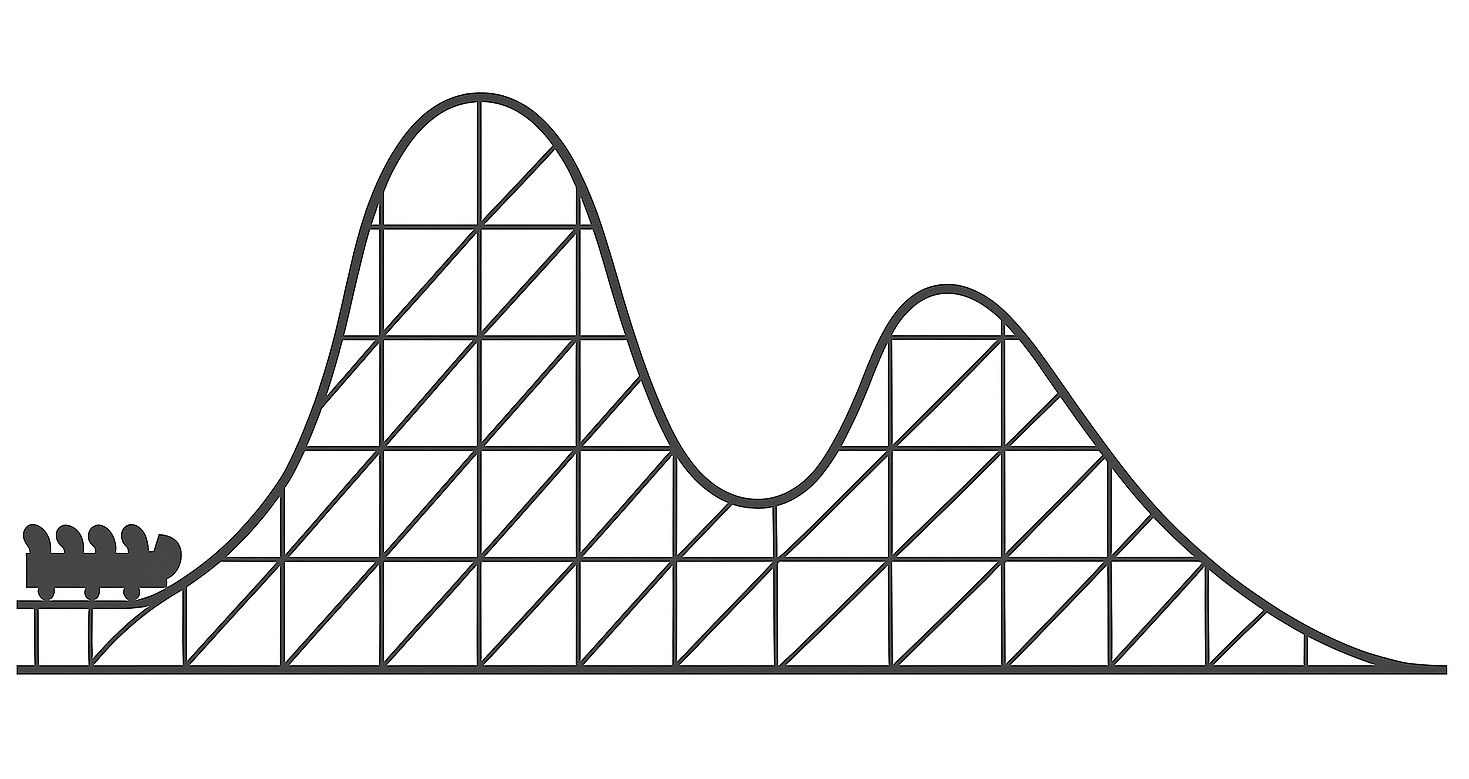
🎢 Monotonie auf Achterbahnschienen
Stell dir eine Achterbahnfahrt vor – aber wir betrachten sie nicht von vorne oder oben, sondern von der Seite:
Wir schauen nur auf den Höhenverlauf des Wagens – also: Wie geht es auf und ab?
Die Fahrt könnte so aussehen:
🔍 Steigungen und Gefälle im Verlauf der Achterbahnfahrt
Wenn wir die Achterbahnfahrt von links nach rechts durchgehen und uns dabei nur den Höhenverlauf anschauen, dann erkennen wir:
Mathematisch gesehen hat diese Bahn
- einen Tiefpunkt (erste Senke),
- zwei Hochpunkte (einer davon global),
- und drei Abschnitte mit waagrechter Strecke (Start, Kuppe, Endstation).
🎢 Abschnitt 1: Vom Start hinauf zum ersten Hügel
Typischerweise wird der Wagen hier mechanisch nach oben gezogen – also eine Phase mit Anstieg. Die Höhe nimmt zu, also ist dieser Abschnitt monoton steigend.
Aber eben nur monoton, nicht streng monoton, und zwar aus folgendem Grund:
Für „streng monoton“ müsste die Steigung überall positiv sein – also auch am Anfang und Ende dieses Abschnitts.
Doch:
In der Station steht der Wagen waagrecht.
Ganz oben auf dem Hügel ist es oft ebenfalls kurz eben
Die Steigung ist an diesen beiden Punkten also null – nicht positiv.
Streng monoton ist der Abschnitt daher nur, wenn man diese beiden Randstellen ausklammert.
🎢 Abschnitt 2: Vom Hügel runter in die Senke
Nach dem Hochpunkt geht’s steil bergab – die Höhe nimmt ab.
Auch hier: monoton fallend, aber nicht streng, denn:
Oben auf dem Hügel ist die Steigung null (Kuppe).
Unten in der Senke ist sie ebenfalls null (Tiefpunkt)
Die Fahrt verläuft also durchgehend fallend, aber mit kurzen waagrechten Stellen – also wieder nicht streng monoton.
Wenn man jedoch den Hochpunkt und den Tiefpunkt nicht mitbetrachtet, ist der Rest streng monoton fallend.
🎢 Abschnitt 3: Der kleine Hügel in der Mitte
Nach der Senke folgt wieder ein Anstieg – wir fahren auf den kleinen Hügel zu.
Auch hier: monoton steigend, mit dem gleichen Hinweis wie zuvor:
Streng monoton wäre es nur, wenn man den Anfang und das Ende des Abschnitts ausklammert – dort ist die Steigung jeweils null.
🎢 Abschnitt 4: Das letzte Gefälle und die Auslaufstrecke
Nach dem letzten Hochpunkt beginnt das längste Gefälle der Bahn. Es geht abwärts bis zur Endstation.
Im Wesentlichen gilt hier dasselbe wie bei Abschnitt 2:
- Die Strecke ist monoton fallend
- Aber sie endet wieder in einem waagrechten Abschnitt an der Station
Also: nicht streng, aber durchgängig fallend – wenn man die waagrechte Endstelle ignoriert, sogar streng monoton fallend.
📌 Fazit: Gesamtverlauf der Schwerkraftstrecke
Wenn wir nur den Teil betrachten, bei dem der Wagen von der Schwerkraft angetrieben wird – also von der Kuppe des Start-Hügels bis zur Endstation –, dann ist das Ganze nicht einmal monoton fallend.
Warum?
Weil zwischendurch noch ein Anstieg kommt – der kleine Hügel in der Mitte.
Dort wird der Wagen kurz wieder höher, bevor er ins letzte Gefälle fährt.
Das heißt:
Insgesamt nimmt die Höhe zwar ab, aber nicht durchgehend.
Die Fahrt ist also nicht monoton, sondern nur:
„im Mittel“ fallend.
🎢 Natürlich nicht im Freizeitpark …
Natürlich stellt sich kein Schüler – auch nicht aus dem Matheleistungskurs – im Freizeitpark an eine Achterbahn und denkt sich:
„Hm … streng monoton fallend – interessant.“
Aber:
Gerade in der Technik ist es sehr wohl von Bedeutung, ob eine Strecke monoton fällt, streng fällt – oder zwischendurch sogar mal flach oder ansteigend verläuft.
Denn:
Wenn der Wagen nach dem Start streng monoton fällt, dann wird er ständig schneller – ohne Pause, ohne Entlastung.
Und das kann schnell gefährlich werden:
- Die Geschwindigkeit steigt immer weiter an
- Die Bremswege verlängern sich
- Und spätestens im anschließenden Kreisel oder Looping wird’s den Fahrgästen schlicht schlecht
Deshalb achten Achterbahnplaner sehr wohl auf so etwas wie Monotonie –
nicht als Gleichung, sondern als Gestaltungsmerkmal:
„Brauchen wir hier eine waagrechte Passage, um die Geschwindigkeit zu dämpfen?“
„Darf es an dieser Stelle wirklich durchgehend steil bergab gehen?“
Und genau an diesem Punkt lohnt es sich auch im Matheunterricht, einmal ganz genau hinzuschauen:
Was bedeutet eigentlich monoton – und was unterscheidet das von streng monoton?
📐 Und jetzt zur Sache: Die Definitionen
Bei monoton steigend oder fallend geht es darum, dass die Funktion sich in eine Richtung entwickelt – also:
- immer höher (steigend) oder
- immer tiefer (fallend)
Aber:
Es darf dabei durchaus Stellen geben, an denen die Steigung null ist – also eine waagrechte Tangente.
Die Funktion darf an solchen Punkten kurz konstant bleiben, ohne den Monotoniebegriff zu verletzen.
Bei streng monoton steigend oder fallend ist das anders:
Hier ist gefordert, dass alle Steigungen echt positiv oder echt negativ sind –
also keine waagrechten Stellen erlaubt sind.
Die Zahl Null ist weder positiv noch negativ. Sie liegt genau zwischen beiden Bereichen – sie ist neutral. Deshalb ist eine Steigung von null zwar erlaubt bei monoton , aber nicht erlaubt bei streng monoton.
Was bedeuten die Punkte in den Grafiken?In den Grafiken ist am Anfang und Ende jedes markierten Abschnitts ein Punkt zu sehen:
- Ausgefüllter Punkt(●): Der Punkt gehört zum betrachteten Abschnitt dazu.
- Leerer Punkt(◯): Der Punkt gehört nicht dazu – er wird beim Betrachten ausgeschlossen.
Diese Darstellung kennt man auch von Intervallen: geschlossen = Punkt gefüllt, offen = Punkt hohl.
🔼 Monoton steigend
Definition: Für alle x₁ < x₂ gilt: f(x₁) ≤ f(x₂)
Erklärung:
– Darf auch waagrecht verlaufen
– Niemals fallend

🔽 Monoton fallend
Definition:
Für alle x₁ < x₂ gilt: f(x₁) ≥ f(x₂)
Erklärung:
– Darf auch waagrecht verlaufen
– Niemals steigen
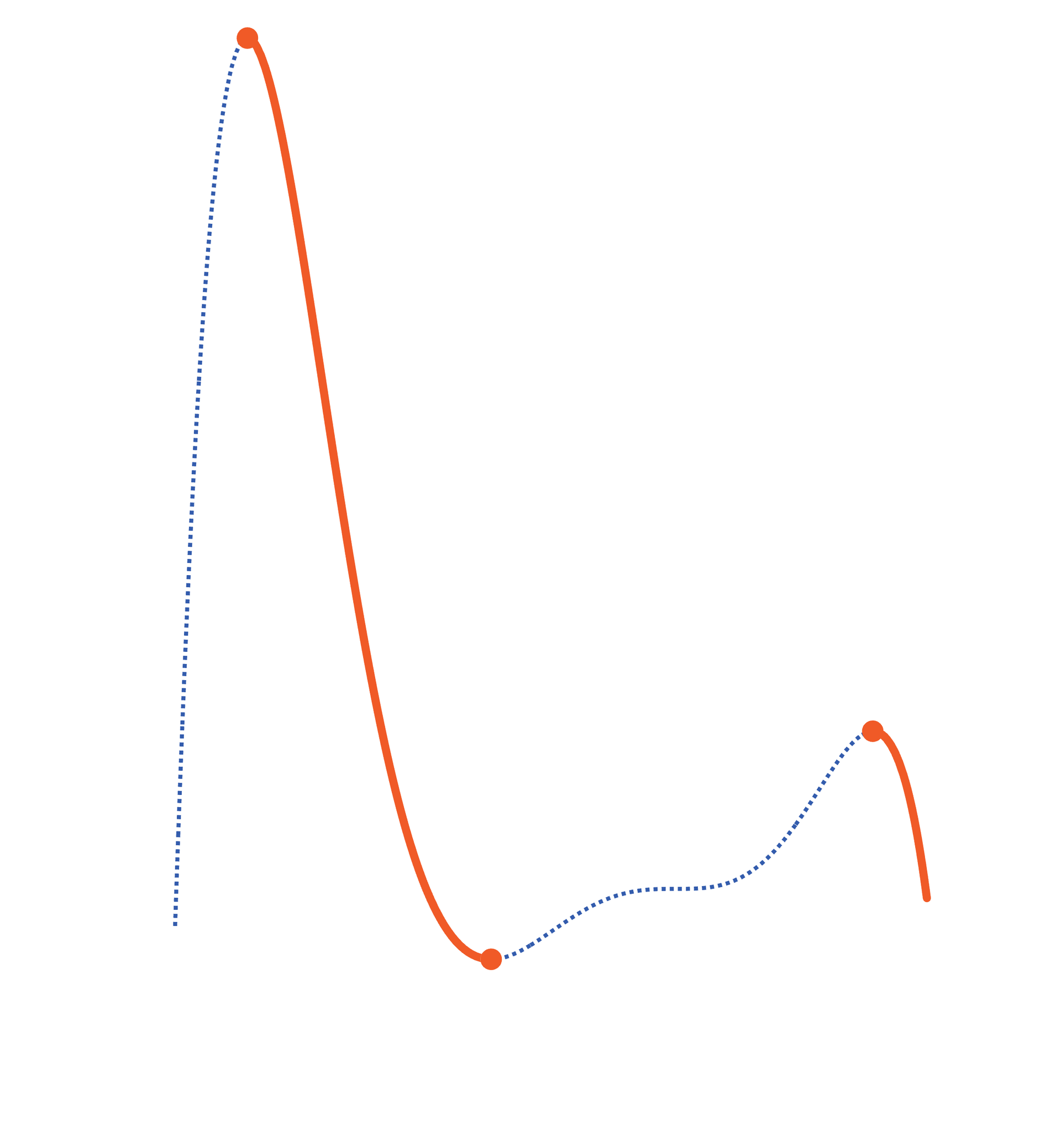
🔽 Streng monoton fallend
Definition:
Für alle x₁ < x₂ gilt: f(x₁) > f(x₂)
Erklärung:
– Muss überall fallen
– Keine waagrechten Stellen erlaubt

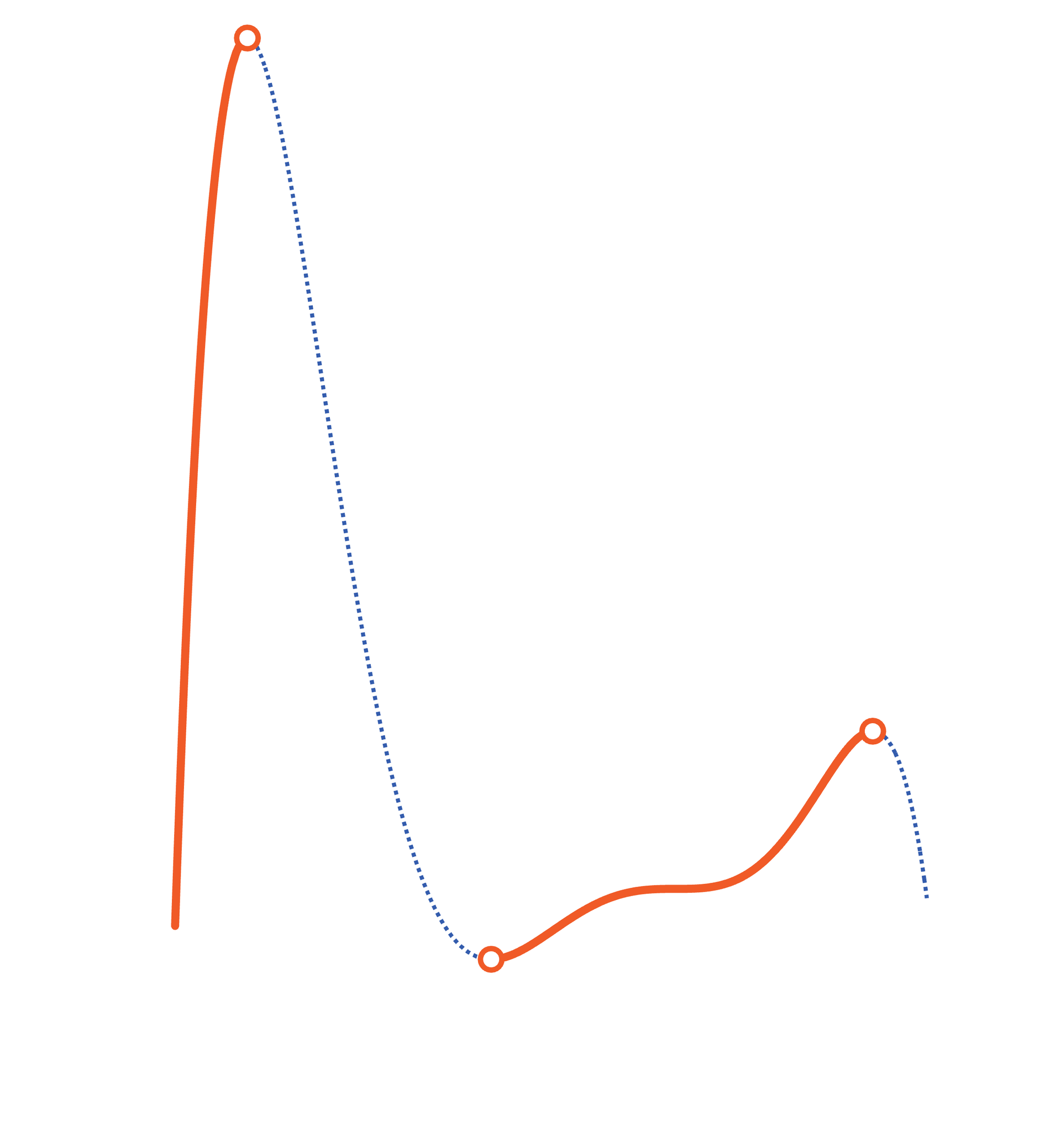
🔼 Streng monoton steigend
Definition:
Für alle x₁ < x₂ gilt: f(x₁) < f(x₂)
Erklärung:
– Muss überall steigen
– Keine waagrechten Stellen erlaubt
Aber das Intervall mit dem Sattelpunkt, ist nur monoton steigend, wegen der Steigung im Sattelpunkt!
🧭 Und wie untersucht man Monotonie jetzt konkret?
Keine Sorge – du musst dafür keine Achterbahnen analysieren.
Was du brauchst, ist eine klare Schritt-für-Schritt-Vorgehensweise:
🔢 Rezept zur Monotonie-Untersuchung:
- Funktion ableiten:
- Bestimme die erste Ableitung f’(x)
- Ableitung gleich null setzen:
- Löse die Gleichung f’(x) = 0
- → Das sind die kritischen Stellen, an denen sich das Steigungsverhalten ändern kann
- Vorzeichen untersuchen:
- Untersuche das Vorzeichen von f’(x) in den Zwischenräumen (also zwischen den Nullstellen)
- – zum Beispiel durch Einsetzen von Testwerten
- Monotonie festlegen:
- Wenn f’(x) > 0 → streng monoton steigend
- Wenn f’(x) < 0 → streng monoton fallend
- Wenn f’(x) = 0 in einem Intervall oder Punkt → nicht streng
🧠 Und warum lohnt sich das?
Weil das genau einer dieser Fälle ist, in denen die Mathematik ihren eigentlichen Zweck erfüllt:
Arbeit vermeiden.
Wenn ich das Monotonieverhalten einer Funktion sauber untersuche,
kann ich damit Extrempunkte zuverlässig erkennen,
ohne mir die Mühe einer zweiten Ableitung zu machen.
Und sind wir ehrlich:
Diese zweite Ableitung ist in vielen Fällen unnötig anstrengend.
Gerade wenn sie aufwendig zu berechnen ist.
Monotonie liefert mir oft genau die Information, die ich brauche –
mit weniger Aufwand zu den geforderten Lösungen.
Transparenzhinweis: Niemand hat die Absicht, ohne ChatGPT einen Blog zu schreiben.

